| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 알래스카 크루즈
- 스웨덴
- 미얀마
- 일본 규슈
- 미국 요세미티
- 중국 베이징
- 프랑스
- 남인도
- 덴마크
- 영국 스코틀랜드
- 러시아
- 싱가포르
- 알래스카
- 독일
- 폴란드
- 헝가리
- ㅓ
- 체코
- 하와이
- 미국 플로리다
- 미국 옐로우스톤
- 울릉도
- 미국 하와이
- 노르웨이
- 알래스카 내륙
- 영국 스코틀랜트
- 영국
- 미국 알래스카
- 1ㄴ
- 오스트리아
- Today
- Total
새샘(淸泉)
실생활에 응용하는 피타고라스 정리2-경제적인 피자 주문 본문
피자 가게에서 두께는 같고 크기만 다른 아래와 같은 세 종류의 피자를 판다.

이때 15,000원으로 큰 판 하나를 주문하는 것이 경제적인지, 아니면 작은 판과 중간 판을 하나씩 주문하는 것이 경제적인지는 다음과 같이 피타고라스 정리를 이용하면 알 수 있다.
1. 자를 이용하여 세 종류 피자 각각의 지름을 재거나, 끈이나 실을 이용하여 지름의 비를 계산한다.
각 판의 피자 크기는 각 길이를 지름으로 가진 원의 넓이가 된다.
2. 지름 길이 또는 지름의 비를 피타고라스 정리를 이용하여 짧은 두 변 각각의 길이 제곱 값의 합과, 가장 긴 변 길이의 제곱 값을 서로 비교한다.
3. 1) 아래 그림에서 처럼 짧은 두 변 각각의 길이 제곱의 합과, 가장 긴 변 길이의 제곱 값이 거의 비슷하면 어떤 선택을 해도 무방하다.
즉 세 변의 비가 3:4:5에 가까우면 어떤 선택이라도 OK.
이 경우 세 변으로 삼각형을 만들면 직각삼각형이 되므로, 짧은 두 변 각각이 이루는 작은 판 및 중간 판 피자의 면적(양)의 합은, 가장 긴 변이 이루는 큰 판 피자의 면적(양)과 같다.

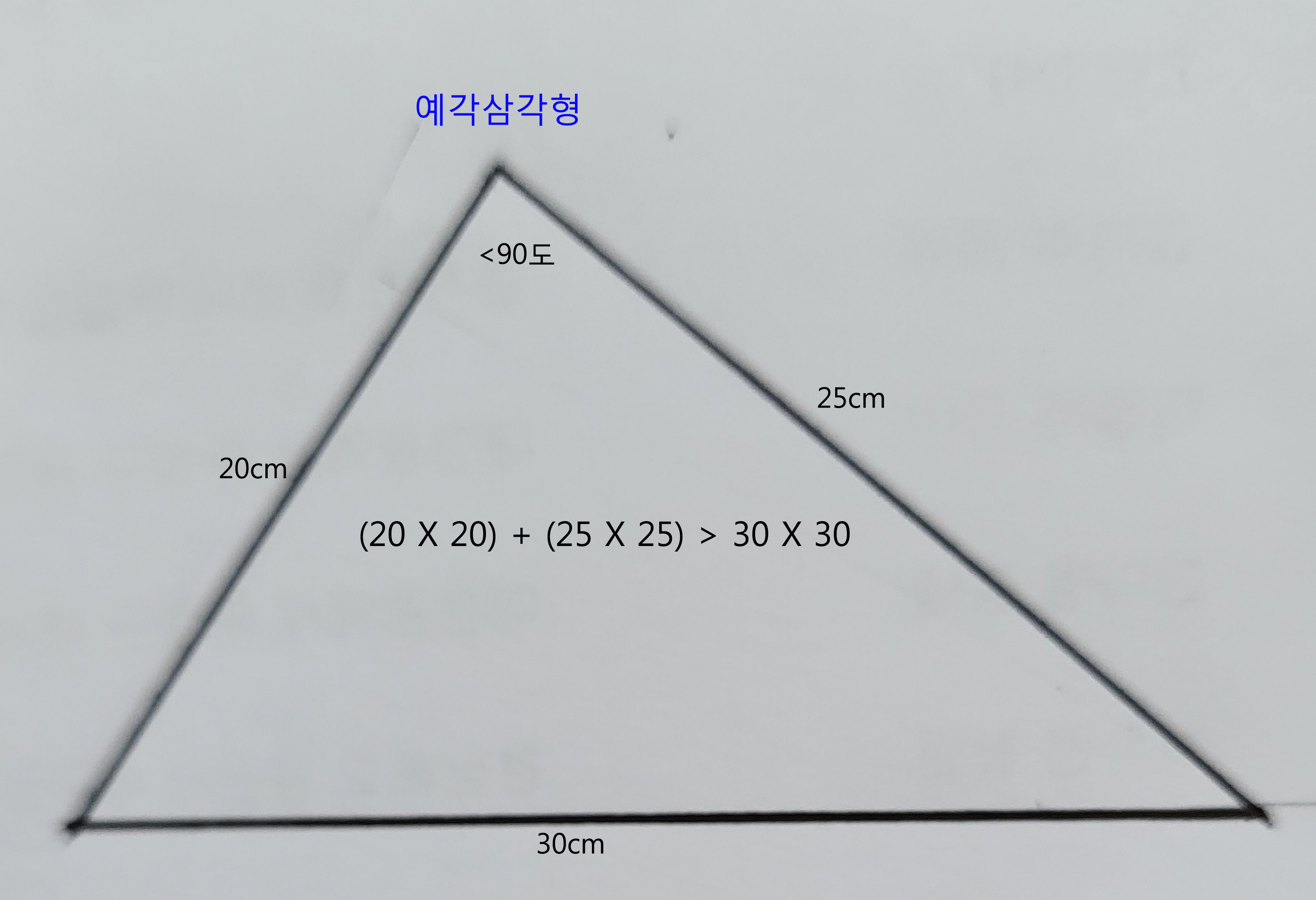
2)만약 짧은 두 변 각각의 길이 제곱의 합이, 가장 긴 변 길이의 제곱 값보다 크면 작은 판과 중간 판 피자 1개씩을 사는 것이 경제적이다.
즉 세 변을 서로 연결하여 삼각형을 만들었을 때 아래 그림과 같은 예각삼각형이 만들어지므로, 짧은 두 변 각각이 이루는 작은 판 및 중간 피자의 면적(양)의 합은, 가장 긴 변이 이루는 큰 판 피자의 면적(양)보다 많다.
따라서 작은 판 피자와 중간 판 피자 1개씩 사는 것이 경제적이다.
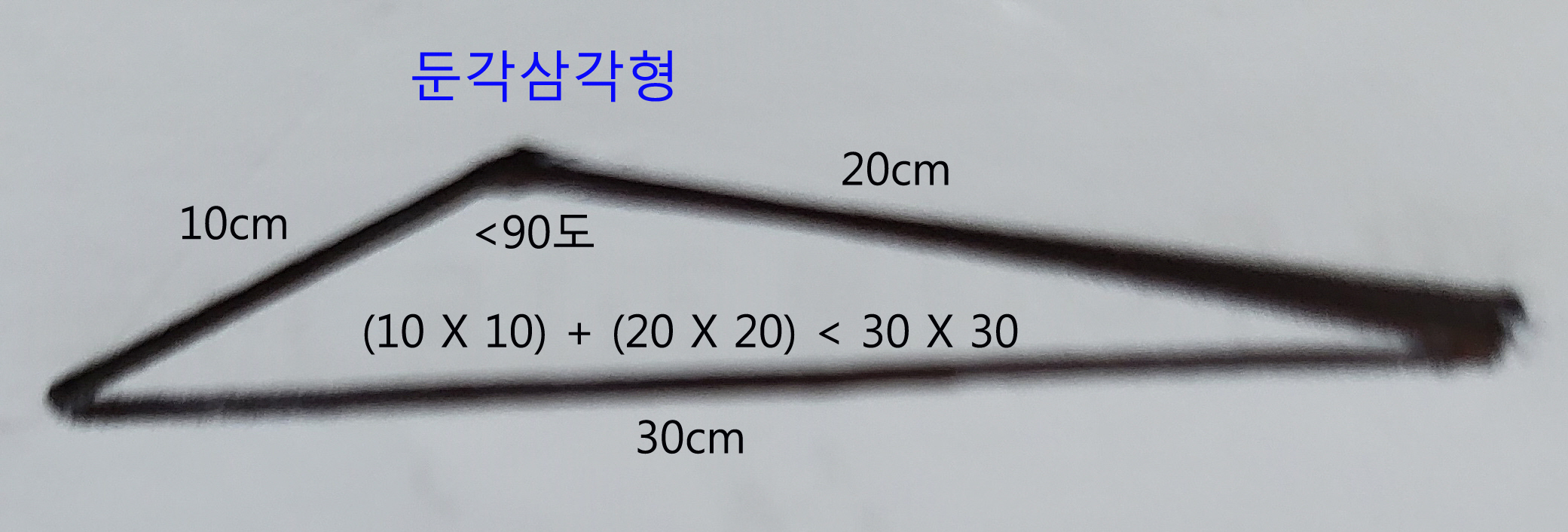
3) 만약 짧은 두 변 각각의 길이 제곱의 합이, 가장 긴 변 길이의 제곱 값보다 작으면 큰 판 1개를 사는 것이 경제적이다.
즉 세 변을 서로 연결하여 삼각형을 만들었을 때 아래 그림과 같은 둔각삼각형이 만들어지므로, 짧은 두 변 각각이 이루는 작은 판 및 중간 피자의 면적(양)의 합은, 가장 긴 변이 이루는 큰 판 피자의 면적(양)보다 적다.
따라서 큰 판 피자 1개를 사는 것이 경제적이다.
※출처
1. 김홍종 지음, '문명, 수학의 필하모니'(효형출판, 2009).
2. 구글 관련 자료
2022. 4. 2 새샘
'글과 그림' 카테고리의 다른 글
| 1990년대 서울에서 발굴된 유적들 9: 용산동 국립중앙박물관 신축부지, 암사동 유적, 신정동 토성, 대모산 유적 (0) | 2022.04.07 |
|---|---|
| 세계 거석문화1: 우리나라 고인돌, 이집트 피라미드와 오벨리스크 (0) | 2022.04.04 |
| 과학기술, 우리가 맞이하게 될 미래 이야기 (0) | 2022.04.01 |
| 코핀과 스테이시의 '새로운 서양문명의 역사' – 1부 고대 근동 - 2장 고대 근동의 신과 제국(서기전 1700~500년) 6: 초기 철기시대의 소국들 (0) | 2022.03.29 |
| 고송유수관도인 이인문 "수옥정도" "단발령망금강도" (0) | 2022.03.28 |





